Pumps normally have sumps that are open to the atmosphere with the liquid level above the suction inlet of the pump, shown in Figure 2.5 1B. In this arrangement, the pressure on the liquid surface is atmospheric and some additional pressure is added by the static elevation head. Unless there is an unusually long or complicated suction piping arrangement, or the liquid is hot, this type of system provides enough positive pressure to prevent the pump from cavitating. However, this arrangement and set of conditions is not always possible and a method of evaluating the suction conditions of a pump must be used to make sure the pump will not cavitate. This is done by determining the absolute pump inlet pressure over the vapor pressure of the liquid and comparing it to the pressure required by the pump to prevent cavitation. These values are known as net positive suction head, or NPSH. The system value is called the net positive suction head available, NPSHA, and the pump value is the net positive suction head required, NPSHR.
Net positive suction head is often misunderstood. The phrase “positive suction head” confuses many people into thinking of the term as simply the static elevation head on the suction of the pump instead of the actual meaning of NPSH. The term describes the absolute pressure above the vapor pressure of the liquid being handled at the suction flange of the pump. It is a study of the energy conditions at the suction flange of the pump to determine if the liquid will vaporize at the lowest pressure area in the system. The concept is abstract, but a few examples and illustrations will make it much easier to understand.
THe NPSH required is the easiest value to understand. It is a value that is published on performance curves by the manufacturer and is a characteristic of the pump’s inlet geometry. Generally, it increases with increasing speed and with increasing flow. The specific value should be read from the performance curve at operating condition point. The values for slurry pumps are usually low, in the range of 1 to 12 meters NPSH required with typical values of 2 to 4 meters. Once this value has been identified, the suction system of the pump installation must be evaluated for the NPSH available to make sure it is greater than the NPSH required by the pump.
The values of NPSH available are unique to each system and flow rate and they must be calculated from detailed information about the system and the liquid being handled. To determine the NPSH available, the vapor pressure of the liquid at the operating temperature must be known. The suction static elevation change, the flow rate, and the details of the the suction piping system must be known in order to calculate the friction losses in the suction system. The pressure on the surface of the suction supply must also be known. It will be atmospheric if the supply is open or will be absolute pressure if the suction supply is delivered from a closed tank.
There are four basic suction system arrangements shown in Figure 2.5-1. Systems can have suction lifts as shown in Figure 2.5-1A and C, or they can have flooded suctions as shown in Figure 2.5-1b and D. If there is a suction lift, some means of priming the pump will be needed before the pump can operate. Each diagram in the figure includes a formula for calculating the NPSH available for each suction arrangement.
The calculation of NPSH available is simply a summation of the terms discussed above. The pressure on the surface of the suction supply is always in absolute terms and is always considered positive. The vapor pressure of the fluid is always a negative term. The friction losses in the suction line always have a negative sign. The static suction head can be either a positive or negative depending upon if the suction is flooded or if there is suction lift. All of the terms are expressed in meters, and when added, yield the NPSH available.
A simple example using Figure 2.5-1B will illustrate this process. The pressure on the liquid surface will be atmospheric and at sea level the value of pa is 1.013 bar or 10.35 meters. It will be assumed that the suction head (Hs)is 3 meters and the losses in the suction line amount to 2.4 meters at the desired flow rate. The liquid being pumped is dirty water at 20 degrees Celsius and has a vapor pressure of .023 bar or .24 meters. The NPSH available is:
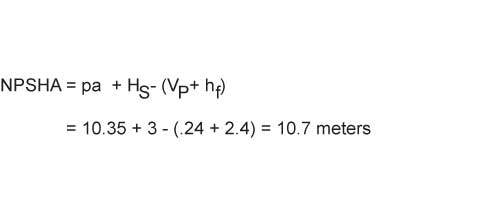 |
This number is compared to the NPSH required, and if it is larger than the NPSHR, the pump will not cavitate. In order to assure a good installation, the NPSHA should be 15 to 30 percent more than the NPSHR. This rule of thumb will allow for some process variations and keep the pump from cavitating.
|
|
Although NPSH is expressed in terms of head, it is a concept based on pressure and this should make it responsive to specific gravity. In slurry pumping, the specific gravity is normally ignored in the calculation of NPSHA when there is a flooded suction. Experiments have shown that the NPSHR on slurry mixtures is the same value as clear water which means that cavitation begins at a higher absolute pressure when handling slurries.
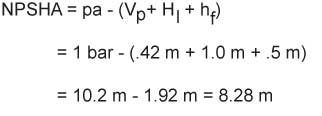 |
In effect, this makes the calculation of NPSHA independent from specific gravity when handling slurries and the suction is flooded; or stated another way, the additional pressure resulting from a specific gravity greater than 1.0 should not be added to the NPSHA. This approach allows the system to be operated on water or with a less concentrated slurry without the danger of cavitation. However, when a suction lift condition exists, the specific gravity must be part of the calculation because it subtracts from the NPSHA.
The pressure resulting from a static column of liquid is a function of the distance below the liquid’s surface and its specific weight. In the case of the suction lift, the problem is reversed to find out what height a liquid can be raised given the pressure on the surface of the liquid. Since centrifugal pumps draw liquid into the eye of the impeller by lowering the pressure at the eye below that of the suction source, the only energy available to move the liquid into the impeller is the differential pressure that the pump has created at the inlet. When the specific gravity is greater than 1.0, part of that differential pressure energy must be used to lift the additional weight of the fluid which reduces the NPSHA.
Sumps that are open to the air have atmospheric pressure available and pumps drawing from closed tanks have the absolute pressure on the liquid’s free surface available to raise the liquid. At sea level, atmospheric pressure will support a column of pure cold water 10.35 meters high against a perfect vacuum. If the water is replaced with a liquid that has a specific gravity of 1.5, the column height will be reduced to 6.9 meters. This change in height is a graphic example of why the specific gravity must be considered in NPSHA calculations when there is a suction lift.
The simplest method of calculating specific gravity on a suction lift installation as shown in Figure 2.5-1A is to divide the pressure on the free surface of the suction supply by the specific gravity. This will reduce the the height of supportable liquid column, or head, as in the example above. The equation given in FIgure 2.5-1A will illustrate two identical cases except for the specific gravity of the liquid.
For an installation pumping clear water at 30 degrees Celsius with a lift of 1 meter, suction piping friction losses of .5 meter and 1 bar pressure on the liquid surface, the available NPSH is:
 |
If all conditions are maintained but the specific gravity is increased to 1.5, the available NPSH will be:
|
|
This example is a good illustration of the importance of considering the specific gravity in the calculation of NPSHA when there is a suction lift application. If a pump with an NPSHR of 6 meters were installed in this system, it will perform without cavitation on water, but when the higher specific gravity slurry is introduced, it will cavitate. Once a pump is installed, it is usually very difficult and expensive to increase the NPSH available to correct a cavitating condition. Avoiding the problem by careful attention to the system design details and pump selection is best.
